1. Вступ

Коли ми говоримо про верстати з CNC, зазвичай маємо на увазі машини, яким дають команду переміститися в певне місце і виконати різні завдання. Щоб мати єдине уявлення про простір верстата і пристосувати його до людського сприйняття тривимірного простору, більшість верстатів (якщо не всі) використовують загальну систему координат, яка називається декартовою системою координат.

Декартова система координат складається з трьох осей (X, Y, Z), кожна з яких перпендикулярна до двох інших. Примітка: [Слово «осі» також часто (і неправильно) використовується при обговоренні верстатів з CNC та згадці про напрямки руху верстата.].

Коли ми говоримо про програму G-коду (RS274/NGC), ми маємо на увазі низку команд (G0, G1 тощо), які мають позиції як параметри (X- Y- Z-). Ці позиції точно відповідають декартовим позиціям. Частина контролера руху LinuxCNC відповідає за перетворення цих позицій у позиції, які відповідають кінематиці верстата примітка:[Кінематика: двостороння функція перетворення з декартового простору в простір з’єднання.].

1.1. Суглоби проти осей

Суглоб верстата з CNC є одним із фізичних ступенів свободи верстата. Він може бути лінійним (гвинтові шнеки) або обертовим (поворотні столи, суглоби маніпулятора робота). На даному верстаті може бути будь-яка кількість суглобів. Наприклад, один популярний робот має 6 суглобів, а типовий простий фрезерний верстат має лише 3.

Існують певні машини, в яких з’єднання розташовані відповідно до кінематичних осей (з’єднання 0 вздовж осі X, з’єднання 1 вздовж осі Y, з’єднання 2 вздовж осі Z), і ці машини називаються декартовими машинами (або машинами з тривіальною кінематикою). Це найпоширеніші машини, що використовуються у фрезеруванні, але вони не дуже поширені в інших сферах управління машинами (наприклад, зварювання: роботи типу puma).

LinuxCNC підтримує осі з назвами: X Y Z A B C U V W. Осі X Y Z зазвичай відносяться до звичайних декартових координат. Осі A B C відносяться до координат обертання навколо осей X Y Z відповідно. Осі U V W відносяться до додаткових координат, які зазвичай є колінеарними до осей X Y Z відповідно.

2. Тривіальна кінематика

Найпростіші машини — це ті, в яких кожен шарнір розміщений вздовж однієї з декартових осей. На цих машинах відображення з декартового простору (програма G-коду) на простір шарнірів (фактичні приводи машини) є тривіальним. Це просте відображення 1:1:

pos->tran.x = joints[0];
pos->tran.y = joints[1];
pos->tran.z = joints[2];

У наведеному вище фрагменті коду можна побачити, як здійснюється відображення: положення по осі X ідентичне суглобу 0, положення по осі Y — суглобу 1 тощо. Вищезазначене стосується прямої кінематики (один напрямок перетворення). Наступний фрагмент коду стосується оберненої кінематики (або оберненого напрямку перетворення):

joints[0] = pos->tran.x;
joints[1] = pos->tran.y;
joints[2] = pos->tran.z;

У LinuxCNC кінематика ідентичності реалізована за допомогою кінематичного модуля «trivkins» і розширена до 9 осей. Стандартні співвідношення між координатами осей і номерами з’єднань такі: примітка:[Якщо верстат (наприклад, токарний) оснащений тільки осями X, Z і A, а файл INI LinuxCNC містить тільки визначення цих 3 з’єднань, то попереднє твердження є хибним. Оскільки наразі ми маємо (joint0=X, joint1=Z, joint2=A), що передбачає joint1=Y. Щоб це працювало в LinuxCNC, просто визначте всі осі (XYZA), тоді LinuxCNC використовуватиме простий цикл в HAL для невикористаної осі Y.] Примітка: [Інший спосіб зробити це — змінити відповідний код і перекомпілювати програмне забезпечення.]

pos->tran.x = joints[0];
pos->tran.y = joints[1];
pos->tran.z = joints[2];
pos->a      = joints[3];
pos->b      = joints[4];
pos->c      = joints[5];
pos->u      = joints[6];
pos->v      = joints[7];
pos->w      = joints[8];

Аналогічно, співвідношення за замовчуванням для оберненої кінематики тривкінів такі:

joints[0] = pos->tran.x;
joints[1] = pos->tran.y;
joints[2] = pos->tran.z;
joints[3] = pos->a;
joints[4] = pos->b;
joints[5] = pos->c;
joints[6] = pos->u;
joints[7] = pos->v;
joints[8] = pos->w;

Перетворення для тривіальної машини "кінсів" (кінематика "трівкінсів") або декартової машини легко виконати за умови, що немає пропусків у використаних літерах осей.

Ситуація дещо ускладнюється, якщо в машині відсутня одна або кілька літер осей. Проблема пропущених літер осей вирішується за допомогою параметра модуля «coordinates=» з модулем trivkins. Номери з’єднань присвоюються послідовно кожній вказаній координаті. Токарний верстат можна описати за допомогою «coordinates=xz». Тоді призначення з’єднань будуть такими:

joints[0] = pos->tran.x
joints[1] = pos->tran.z

Використання параметра «coordinates=» рекомендується для конфігурацій, в яких не вказані літери осей. Примітка: Історично модуль trivkins не підтримував параметр «coordinates=», тому конфігурації токарних верстатів часто налаштовувалися як машини XYZ. Невикористана вісь Y налаштовувалася на 1) негайне повернення в початкове положення, 2) використання простого зворотного зв’язку для підключення виводу HAL команди положення до виводу HAL зворотного зв’язку положення, і 3) приховування в графічному інтерфейсі. Численні конфігурації sim використовують ці методи для спільного використання загальних файлів HAL.]

Модуль кінематики «trivkins» також дозволяє вказати одну і ту ж координату для декількох з’єднань. Ця функція може бути корисною на таких машинах, як портал з двома незалежними двигунами для координати y. Така машина може використовувати «coordinates=xyyz», що призведе до призначення з’єднань:

joints[0] = pos->tran.x
joints[1] = pos->tran.y
joints[2] = pos->tran.y
joints[3] = pos->tran.z

Дивіться сторінки довідки trivkins для отримання додаткової інформації.

3. Нетривіальна кінематика

Існує чимало типів налаштувань машин (роботи: puma, scara; гексаподи тощо). Кожен з них налаштовується за допомогою лінійних і поворотних з’єднань. Ці з’єднання зазвичай не відповідають декартовим координатам, тому нам потрібна кінематична функція, яка виконує перетворення (насправді 2 функції: пряма і обернена кінематична функція).

Для ілюстрації вищесказаного розглянемо просту кінематику під назвою сошка (спрощена версія штатива, яка є спрощеною версією гексапода).

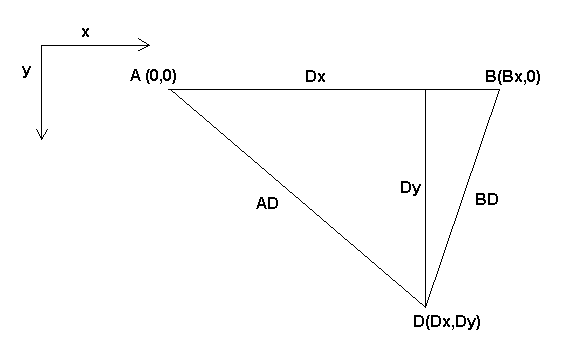
Налаштування сошок
Figure 1. Налаштування сошок

Двонога, про яку ми говоримо, — це пристрій, що складається з 2 двигунів, розміщених на стіні, до яких за допомогою дроту підвішено пристрій. У цьому випадку суглобами є відстані від двигунів до пристрою (на малюнку позначені AD і BD).

Положення двигунів фіксується за угодою. Двигун A знаходиться в точці (0,0), що означає, що його координата X дорівнює 0, а координата Y також дорівнює 0. Двигун B розміщений в точці (Bx, 0), що означає, що його координата X дорівнює Bx.

Наша підказка буде в точці D, яка визначається відстанями AD та BD, а також декартовими координатами Dx, Dy.

Завдання кінематики полягає в перетворенні довжин суглобів (AD, BD) на декартові координати (Dx, Dy) і навпаки.

3.1. Пряма трансформація

Для перетворення з простору суглобів у декартовий простір ми скористаємося деякими правилами тригонометрії (прямокутні трикутники, визначені точками (0,0), (Dx,0), (Dx,Dy) та трикутниками (Dx,0), (Bx,0) та (Dx,Dy)).

Ми можемо легко побачити, що:

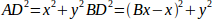
images/kinematics-math-01.png

так само:

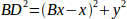
images/kinematics-math-02.png

Якщо відняти одне від іншого, то отримаємо:

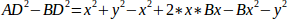
images/kinematics-math-03.png

і тому:

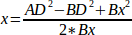
images/kinematics-math-04.png

Звідти ми обчислюємо:

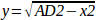
images/kinematics-math-05.png

Зверніть увагу, що обчислення для y включає квадратний корінь з різниці, що може не давати дійсного числа. Якщо для цього положення з’єднання немає єдиної декартової координати, то таке положення називається сингулярністю. У цьому випадку пряма кінематика повертає -1.

Перекладено у фактичний код:

double AD2 = joints[0] * joints[0];
double BD2 = joints[1] * joints[1];
double x = (AD2 - BD2 + Bx * Bx) / (2 * Bx);
double y2 = AD2 - x * x;
if(y2 < 0) return -1;
pos->tran.x = x;
pos->tran.y = sqrt(y2);
return 0;

3.2. Зворотне перетворення

Зворотна кінематика в нашому прикладі набагато простіше, оскільки ми можемо записати її безпосередньо:

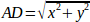
images/kinematics-math-06.png
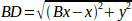
images/kinematics-math-07.png

або переведено у фактичний код:

double x2 = pos->tran.x * pos->tran.x;
double y2 = pos->tran.y * pos->tran.y;
joints[0] = sqrt(x2 + y2);
joints[1] = sqrt((Bx - pos->tran.x)*(Bx - pos->tran.x) + y2);
return 0;

4. Деталі впровадження

Кінематичний модуль реалізовано як компонент HAL і має дозвіл на експорт виводів та параметрів. Він складається з кількох функцій "C" (на відміну від функцій HAL):

int kinematicsForward(const double *joint, EmcPose *world,
const KINEMATICS_FORWARD_FLAGS *fflags,
KINEMATICS_INVERSE_FLAGS *iflags)

Реалізує функцію forward kinematics.

int kinematicsInverse(const EmcPose * world, double *joints,
const KINEMATICS_INVERSE_FLAGS *iflags,
KINEMATICS_FORWARD_FLAGS *fflags)

Реалізує обернену кінематичну функцію.

KINEMATICS_TYPE kinematicsType(void)

Повертає ідентифікатор типу кінематики, типовий варіант KINEMATICS_BOTH:

  1. KINEMATICS_IDENTITY (кожен номер шарніра відповідає літері осі)

  2. KINEMATICS_BOTH (надаються прямі та зворотні кінематичні функції)

  3. KINEMATICS_FORWARD_ONLY

  4. KINEMATICS_INVERSE_ONLY

Note
 Графічні інтерфейси можуть інтерпретувати KINEMATICS_IDENTITY, щоб приховати відмінності між номерами шарнірів та літерами осей у режимі шарніра (зазвичай перед переміщенням до початкової точки). 
int kinematicsSwitchable(void)
int kinematicsSwitch(int switchkins_type)
KINS_NOT_SWITCHABLE

Функція kinematicsSwitchable() повертає 1, якщо підтримується кілька типів кінематики. Функція kinematicsSwitch() вибирає тип кінематики. Див. Switchable Kinematitcs.

Note
 Більшість наданих кінематичних модулів підтримують один тип кінематики і використовують директиву "KINS_NOT_SWITCHABLE" для надання значень за замовчуванням для необхідних функцій kinematicsSwitchable() і kinematicsSwitch(). 
int kinematicsHome(EmcPose *world, double *joint,
KINEMATICS_FORWARD_FLAGS *fflags,
KINEMATICS_INVERSE_FLAGS *iflags)

Функція кінематики вихідного положення встановлює всі свої аргументи на відповідні значення у відомому вихідному положенні. При виклику ці значення повинні бути встановлені, якщо вони відомі, на початкові значення, наприклад, з файлу INI. Якщо кінематика вихідного положення може приймати довільні початкові точки, слід використовувати ці початкові значення.

int rtapi_app_main(void)
void rtapi_app_exit(void)

Це стандартні функції налаштування та демонтажу модулів RTAPI.

Коли кінематичні модулі містяться в одному вихідному файлі, їх можна скомпілювати та встановити за допомогою «halcompile». Див. сторінку довідки «halcompile(1)» або посібник HAL для отримання додаткової інформації.

4.1. Кінематичний модуль з використанням шаблону userkins.comp

Інший спосіб створити власний кінематичний модуль – це адаптувати компонент HAL «userkins». Цей шаблонний компонент може бути змінений локально користувачем і може бути зібраний за допомогою halcompile.

Дивіться сторінки довідки userkins для отримання додаткової інформації.

Зауважте, що для створення перемиканих кінематичних модулів необхідні модифікації дещо складніші.

Див. «millturn.comp» як приклад перемиканого кінематичного модуля, створеного за допомогою шаблону «userkins.comp».