1. Einführung
Koordinierte mehrachsige CNC-Werkzeugmaschinen, die mit LinuxCNC gesteuert werden, erfordern eine spezielle Kinematikkomponente für jede Art von Maschine. Dieses Kapitel beschreibt einige der gängigsten 5-Achsen-Maschinenkonfigurationen und entwickelt dann die Vorwärts- (von Arbeits- zu Gelenkkoordinaten) und Rückwärtstransformationen (von Gelenk zu Arbeit) in einem allgemeinen mathematischen Prozess für zwei Maschinentypen.
Die kinematischen Komponenten werden ebenso dargestellt wie Vismach-Simulationsmodelle, um ihr Verhalten auf dem Computerbildschirm zu demonstrieren. Es werden auch Beispiele für HAL-Dateien gegeben.
Beachten Sie, dass sich bei dieser Kinematik die Rotationsachsen in die entgegengesetzte Richtung bewegen, wie es die Konvention vorsieht. Siehe Abschnitt ["Rotationsachsen"] (https://linuxcnc.org/docs/html/gcode/machining-center.html#_rotational_axes) für Details.
2. 5-Achsen-Werkzeugmaschinen-Konfigurationen
In diesem Abschnitt befassen wir uns mit den typischen 5-Achsen-Fräs- oder Oberfräsmaschinen mit fünf Gelenken oder Freiheitsgraden, die in koordinierten Bewegungen gesteuert werden.
3-Achsen-Werkzeugmaschinen können die Werkzeugausrichtung nicht ändern, daher verwenden 5-Achsen-Werkzeugmaschinen zwei zusätzliche Achsen, um das Schneidwerkzeug in eine geeignete Ausrichtung für die effiziente Bearbeitung von Freiformflächen zu bringen.
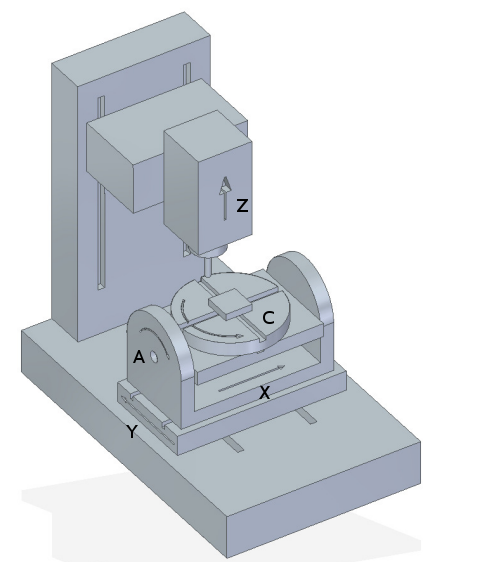
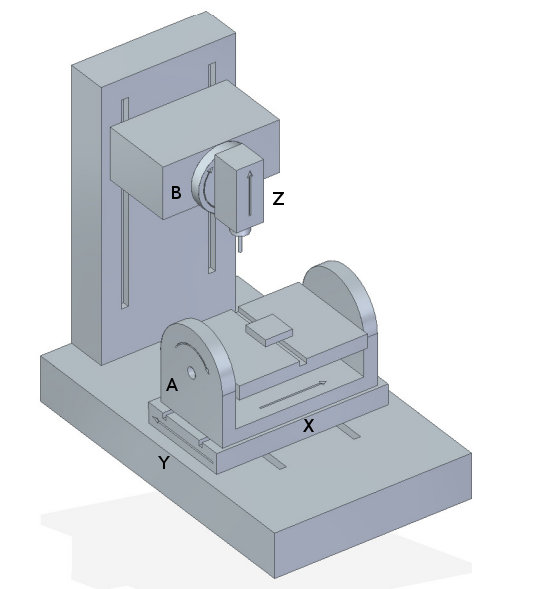
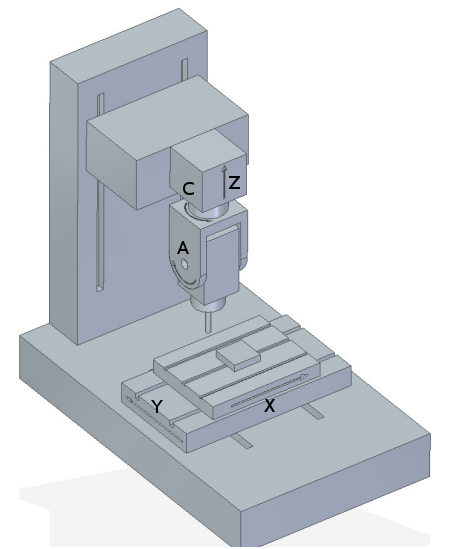
Typische Konfigurationen von 5-Achsen-Werkzeugmaschinen sind in den Abbildungen 3, 5, 7 und 9-11 [1,2] im Abschnitt Abbildungen dargestellt.
Die Kinematik von 5-Achsen-Werkzeugmaschinen ist viel einfacher als die von 6-Achsen-Serienarmrobotern, da 3 der Achsen normalerweise lineare Achsen und nur zwei rotierende Achsen sind.
3. Werkzeugausrichtung und -position
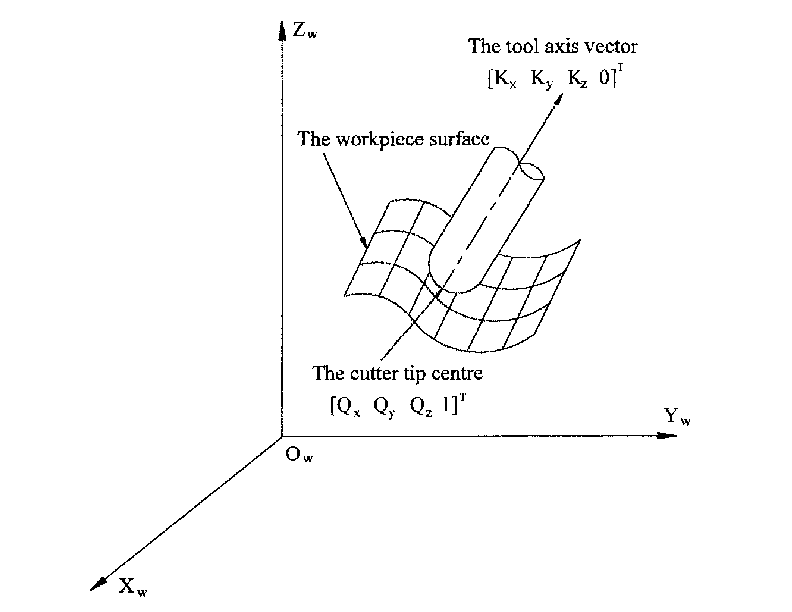
CAD/CAM-Systeme werden in der Regel verwendet, um die 3D-CAD-Modelle des Werkstücks sowie die CAM-Daten für die Eingabe in die CNC-5-Achsen-Maschine zu erzeugen. Die Daten zur Werkzeug- oder Fräserposition (CL) setzen sich aus der Position der Fräserspitze und der Ausrichtung des Fräsers relativ zum Werkstückkoordinatensystem zusammen. Zwei Vektoren, wie sie von den meisten CAM-Systemen erzeugt werden und in Abb. 1 dargestellt sind, enthalten diese Informationen:
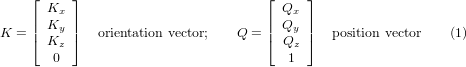
Der K-Vektor entspricht dem dritten Vektor der Pose-Matrix E6, die in der 6-Achsen-Roboterkinematik [3] verwendet wurde, und der Q-Vektor entspricht dem vierten Vektor von E6. Vektor von E6. In MASTERCAM zum Beispiel sind diese Informationen in der Zwischenausgabedatei ".nci" enthalten.
4. Translations- und Rotationsmatrizen
Homogene Transformationen bieten eine einfache Möglichkeit, die Mathematik der Mehrachsenkinematik von Maschinen zu beschreiben. Eine Transformation des Raums H ist eine 4x4-Matrix und kann Translations- und Rotationstransformationen darstellen. Wird ein Punkt x,y,x durch einen Vektor u = {x,y,z,1}T beschrieben, so wird seine Transformation v durch das Matrixprodukt
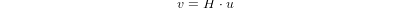
Es gibt vier grundlegende Transformationsmatrizen, auf die sich die 5-Achsen-Kinematik stützen kann:
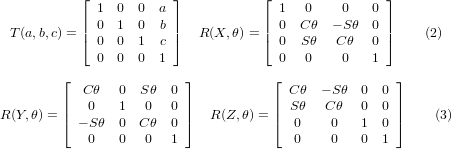
Die Matrix T(a,b,c) impliziert eine Verschiebung in den Koordinatenrichtungen X, Y und Z um die Beträge a, b bzw. c. Die R-Matrizen implizieren Rotationen des Winkels theta um die X-, Y- bzw. Z-Koordinatenachse. Die Symbole "C" und "S" beziehen sich auf die Kosinus- bzw. Sinusfunktionen.
5. Tisch Dreh-/Schwenkkonfigurationen mit 5 Achsen (engl. Table Rotary/Tilting 5-Axis Configurations)
Bei diesen Werkzeugmaschinen sind die beiden Rotationsachsen auf dem Arbeitstisch der Maschine montiert. Typischerweise werden zwei Formen verwendet:
-
Ein Drehtisch, der sich um die vertikale Z-Achse dreht (C-Drehung, sekundär), ist auf einem Kipptisch montiert, der sich um die X- oder Y-Achse dreht (A- oder B-Drehung, primär). Das Werkstück ist auf dem Drehtisch montiert.
-
Ein Kipptisch, der sich um die X- oder Y-Achse dreht (A- oder B-Drehung, sekundär), ist auf einem Drehtisch montiert, der sich um die Z-Achse dreht (C-Drehung, primär), wobei das Werkstück auf dem Kipptisch liegt.

Eine mehrachsige Maschine kann als eine Reihe von Gliedern betrachtet werden, die durch Gelenke verbunden sind. Durch die Einbettung eines Koordinatenrahmens in jedes Glied der Maschine und die Verwendung homogener Transformationen können wir die relative Position und Orientierung zwischen diesen Koordinatenrahmen beschreiben
Wir müssen eine Beziehung zwischen dem Werkstückkoordinatensystem und dem Werkzeugkoordinatensystem beschreiben. Dies kann durch eine Transformationsmatrix "wAt" definiert werden, die durch nachfolgende Transformationen zwischen den verschiedenen Strukturelementen oder Gliedern der Maschine, die jeweils ihr eigenes definiertes Koordinatensystem haben, gefunden werden kann. Im Allgemeinen kann eine solche Transformation wie folgt aussehen:
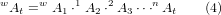
wobei jede Matrix i-1Aj eine Translationsmatrix T oder eine Rotationsmatrix R der Form (2,3) ist.
Die Matrixmultiplikation ist ein einfacher Vorgang, bei dem die Elemente jeder Zeile der linken Matrix A mit den Elementen jeder Spalte der rechten Matrix B multipliziert und summiert werden, um ein Element der Ergebnismatrix C zu erhalten.
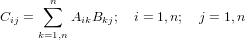
In Abb. 2 ist eine generische Konfiguration mit Koordinatensystemen dargestellt [4]. Sie umfasst sowohl Tischdreh-/Schwenkachsen als auch Spindel-Dreh-/Schwenkachsen. Nur zwei der Drehachsen werden tatsächlich in einer Werkzeugmaschine verwendet.
Zunächst werden wir die Transformationen für die erste der oben erwähnten Konfigurationen entwickeln, d. h. einen Tisch vom Typ Kippen/Drehen (trt) ohne Drehachsenversatz. Wir können ihr den Namen xyzac-trt-Konfiguration geben.
Wir entwickeln auch die Transformationen für den gleichen Typ (xyzac-trt), aber mit rotierenden Achsenversätzen.
Dann entwickeln wir die Transformationen für eine xyzbc-trt-Konfiguration mit Rotationsachsen-Offsets.
5.1. Transformationen für eine xyzac-trt-Werkzeugmaschine mit Werkstückversatz

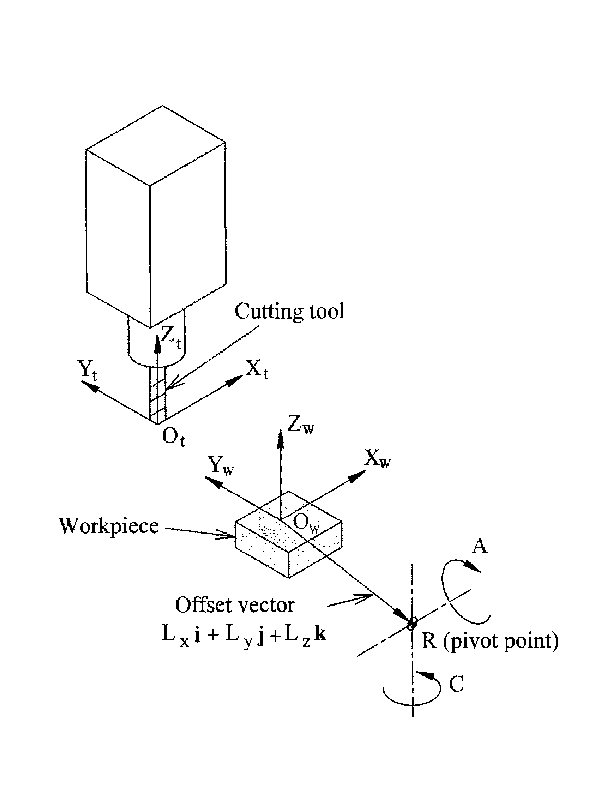
Wir befassen uns hier mit einer vereinfachten Konfiguration, bei der sich die Kippachse und die Drehachse in einem Punkt schneiden, der als Drehpunkt bezeichnet wird, wie in Abb. 4 dargestellt.
5.1.1. Vorwärts-Transformation
Die Transformation kann durch die sequentielle Multiplikation der Matrizen definiert werden:
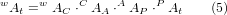
wobei die Matrizen wie folgt aufgebaut sind:
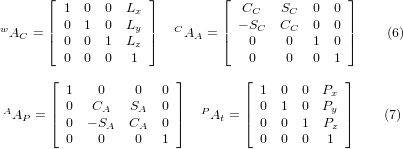
In diesen Gleichungen definieren Lx, Ly, Lz die Verschiebungen des Drehpunktes der beiden Drehachsen A und C relativ zum Ursprung des Werkstückkoordinatensystems. Außerdem sind Px, Py, Pz die relativen Abstände des Drehpunkts zur Position der Fräserspitze, die auch als "Gelenkkoordinaten" des Drehpunkts bezeichnet werden können. Der Drehpunkt liegt im Schnittpunkt der beiden Drehachsen. Die Vorzeichen der Terme SA und SC unterscheiden sich von denen in [2,3], da dort die Tischdrehungen relativ zu den Werkstückkoordinatenachsen negativ sind (beachten Sie, dass sin(-theta) = -sin(theta), cos(-theta) = cos(theta)).
Multipliziert mit (5) ergibt sich das Ergebnis:
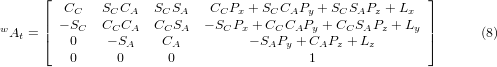
Wir können nun die dritte Spalte dieser Matrix mit unserem gegebenen Werkzeugorientierungsvektor K gleichsetzen, d. h.:
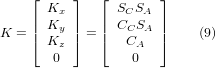
Aus diesen Gleichungen lassen sich die Drehwinkel thetaA, thetaC ermitteln. Aus der dritten Zeile finden wir:
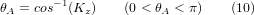
und durch Division der ersten Zeile durch die zweite Zeile ergibt sich:

Diese Beziehungen werden normalerweise im CAM-Postprozessor verwendet, um die Vektoren der Werkzeugausrichtung in Drehwinkel umzuwandeln.
Indem wir die letzte Spalte von (8) mit dem Werkzeugpositionsvektor Q gleichsetzen, können wir schreiben:
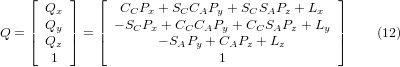
Der Vektor auf der rechten Seite kann auch als das Produkt einer Matrix und eines Vektors geschrieben werden, was folgendes ergibt:
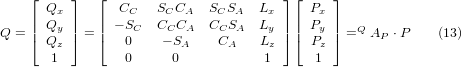
Dies kann wie folgt erweitert werden
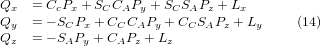
was die Vorwärtstransformation der Kinematik darstellt.
5.1.2. Inverse Transformation
Wir können P aus Gleichung (13) als "P = (QAP)-1 * Q" berechnen. Die quadratische Matrix ist eine homogene 4x4-Matrix, die eine Rotationsmatrix R und einen Translationsvektor q enthält, deren Umkehrung wie folgt geschrieben werden kann:
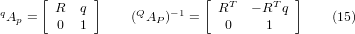
wobei R^T die Transponierung von R ist (Zeilen und Spalten vertauscht). Wir erhalten also:
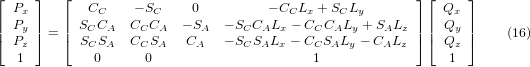
Die gewünschten Gleichungen für die inverse Transformation der Kinematik können somit wie folgt geschrieben werden:
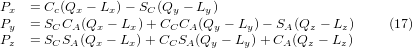
5.2. Transformationen für eine xyzac-trt-Maschine mit Drehachsenverschiebungen
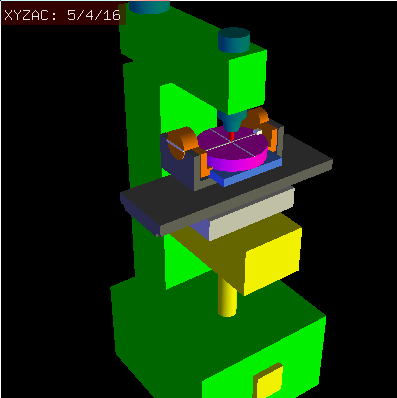
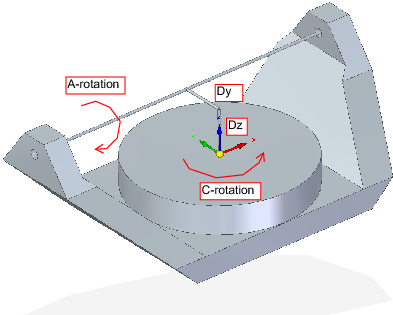
Wir haben es hier mit einer erweiterten Konfiguration zu tun, bei der sich die Kippachse und die Drehachse nicht in einem Punkt schneiden, sondern einen Versatz Dy aufweisen. Außerdem gibt es zwischen den beiden Koordinatensystemen Ows und Owp aus Abb. 2 einen z-Versatz, der Dz genannt wird. Ein Vismach-Modell ist in Abb. 5 dargestellt, und die Offsets sind in Abb. 6 gezeigt (positive Offsets in diesem Beispiel). Um die Konfiguration zu vereinfachen, werden die Versätze Lx, Ly, Lz des vorherigen Falls nicht berücksichtigt. Sie sind wahrscheinlich nicht notwendig, wenn man die G54 Offsets in LinuxCNC mit Hilfe der "touch of"-Funktion verwendet.
5.2.1. Vorwärts-Transformation
Die Transformation kann durch die sequentielle Multiplikation der Matrizen definiert werden:
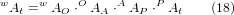
wobei die Matrizen wie folgt aufgebaut sind:
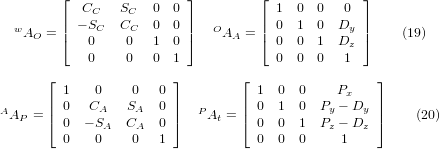
In diesen Gleichungen definieren Dy, Dz die Verschiebungen des Drehpunktes der Drehachsen A relativ zum Ursprung des Werkstückkoordinatensystems. Außerdem sind Px, Py, Pz die relativen Abstände des Drehpunkts zur Position der Schneidenspitze, die auch als "Gelenkkoordinaten" des Drehpunkts bezeichnet werden können. Der Drehpunkt liegt auf der Drehachse A.
Bei Multiplikation gemäß (18) erhalten wir:
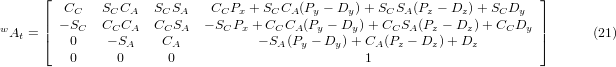
Wir können nun die dritte Spalte dieser Matrix mit unserem gegebenen Werkzeugorientierungsvektor K gleichsetzen, d. h.:
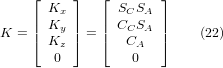
Aus diesen Gleichungen lassen sich die Drehwinkel thetaA, thetaC ermitteln. Aus der dritten Zeile finden wir:
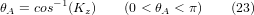
und durch Division der zweiten Zeile durch die erste Zeile ergibt sich:

Diese Beziehungen werden normalerweise im CAM-Postprozessor verwendet, um die Vektoren der Werkzeugausrichtung in Drehwinkel umzuwandeln.
Wenn wir die letzte Spalte von (21) mit dem Werkzeugpositionsvektor Q gleichsetzen, können wir schreiben:
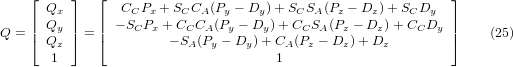
Der Vektor auf der rechten Seite kann auch als das Produkt einer Matrix und eines Vektors geschrieben werden, was folgendes ergibt:
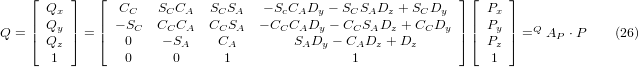
was die Vorwärtstransformation der Kinematik darstellt.
5.2.2. Inverse Transformation
Wir können P aus Gleichung (25) als "P = (QAP)-1 * Q" lösen, indem wir wie zuvor (15) verwenden. Wir erhalten somit:
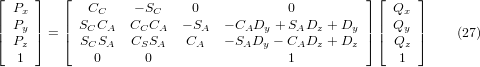
Die gewünschten Gleichungen für die inverse Transformation der Kinematik können somit wie folgt geschrieben werden:
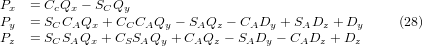
5.3. Transformationen für eine xyzbc-trt-Maschine mit Drehachsenverschiebungen

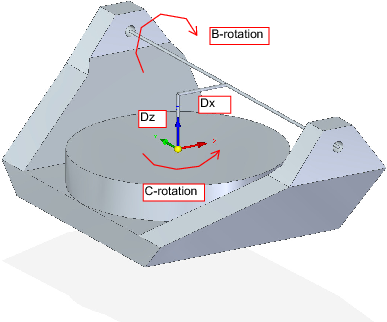
Wir haben es hier wieder mit einer erweiterten Konfiguration zu tun, bei der sich die Kippachse (um die y-Achse) und die Drehachse nicht in einem Punkt schneiden, sondern einen Versatz Dx haben. Außerdem gibt es zwischen den beiden Koordinatensystemen Ows und Owp aus Abb. 2 einen z-Versatz, der Dz genannt wird. Ein Vismach-Modell ist in Abb. 7 dargestellt (negative Versätze in diesem Beispiel), und die positiven Versätze sind in Abb. 8 dargestellt.
5.3.1. Vorwärts-Transformation
Die Transformation kann durch die sequentielle Multiplikation der Matrizen definiert werden:
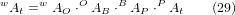
wobei die Matrizen wie folgt aufgebaut sind:
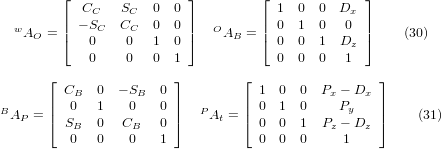
In diesen Gleichungen definieren Dx, Dz die Verschiebungen des Drehpunkts der Drehachsen B relativ zum Ursprung des Werkstückkoordinatensystems. Außerdem sind Px, Py, Pz die relativen Abstände des Drehpunkts zur Position der Schneidenspitze, die auch als "Gelenkkoordinaten" des Drehpunkts bezeichnet werden können. Der Drehpunkt liegt auf der B-Drehachse.
Bei Multiplikation gemäß (29) erhalten wir:
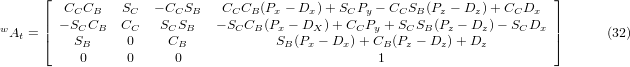
Wir können nun die dritte Spalte dieser Matrix mit unserem gegebenen Werkzeugorientierungsvektor K gleichsetzen, d. h.:
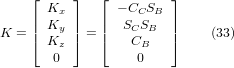
Aus diesen Gleichungen lassen sich die Drehwinkel thetaB, thetaC ermitteln. Aus der dritten Zeile finden wir:
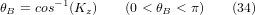
und durch Division der zweiten Zeile durch die erste Zeile ergibt sich:

Diese Beziehungen werden normalerweise im CAM-Postprozessor verwendet, um die Vektoren der Werkzeugausrichtung in Drehwinkel umzuwandeln.
Wenn wir die letzte Spalte von (32) mit dem Werkzeugpositionsvektor Q gleichsetzen, können wir schreiben:
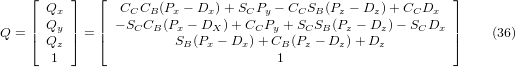
Der Vektor auf der rechten Seite kann auch als das Produkt einer Matrix und eines Vektors geschrieben werden, was folgendes ergibt:
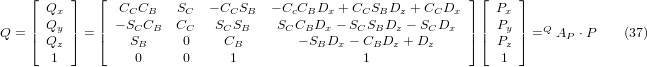
was die Vorwärtstransformation der Kinematik darstellt.
5.3.2. Inverse Transformation
Wir können P aus Gleichung (37) als "P = (QAP)-1 * Q" lösen.
Mit dem gleichen Ansatz wie zuvor, erhalten wir:
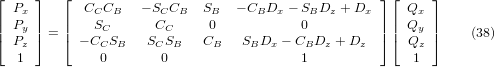
Die gewünschten Gleichungen für die inverse Transformation der Kinematik können somit wie folgt geschrieben werden:
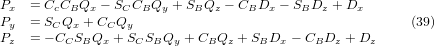
6. Beispiele für Dreh-/Kipptische
LinuxCNC enthält Kinematik-Module für die "xyzac-trt" und "xyzbc-trt" Topologien in der Mathematik oben beschrieben. Für interessierte Benutzer ist der Quellcode im Git-Baum im Verzeichnis "src/emc/kinematics/" verfügbar.
Beispielkonfigurationen für xyzac-trt und xyzbc-trt befinden sich im Verzeichnis Beispielkonfigurationen (configs/sim/axis/vismach/5axis/table-rotary-tilting/).
Die Beispielkonfigurationen enthalten die erforderlichen INI-Dateien und ein Beispiel-Unterverzeichnis mit G-Code (NGC) Dateien. Diese sim Konfigurationen rufen ein realistisches 3-dimensionales Modell mit LinuxCNC vismach.
6.1. Vismach Simulationsmodelle
Vismach ist eine Bibliothek von Python-Routinen zur Darstellung einer dynamischen Simulation einer CNC-Maschine auf dem PC-Bildschirm. Das Python-Skript für eine bestimmte Maschine wird in HAL geladen und die Daten werden über HAL-Pin-Verbindungen übergeben. Das Nicht-Echtzeit-Vismach-Modell wird durch einen HAL-Befehl wie folgt geladen:
loadusr -W xyzac-trt-gui
und Verbindungen werden mit HAL-Befehlen hergestellt wie:
net :table-x joint.0.pos-fb xyzac-trt-gui.table-x
net :saddle-y joint.1.pos-fb xyzac-trt-gui.saddle-y
...Einzelheiten zu den HAL-Verbindungen, die für das Vismach-Modell verwendet werden, finden Sie in den INI-Dateien für die Simulation.
6.2. Werkzeuglängenkompensation
Um Werkzeuge aus einer Werkzeugtabelle sequentiell mit Werkzeuglängenkompensation automatisch angewendet zu verwenden, ist ein weiterer Z-Offset erforderlich. Für ein Werkzeug, das länger ist als die "Master"-Werkzeug, das typischerweise eine Werkzeuglänge von Null zugewiesen wurde, hat LinuxCNC eine Variable namens "motion.tooloffset.z". Wenn diese Variable auf die kinematische Komponente (und vismach Python-Skript) übergeben wird, dann kann die notwendige zusätzliche Z-Offset für ein neues Werkzeug berücksichtigt werden, indem Sie die Komponente Anweisung, zum Beispiel:
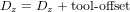
Die erforderliche HAL-Verbindung (für xyzac-trt) ist:
net :tool-offset motion.tooloffset.z xyzac-trt-kins.tool-offset
wo:
:tool-offset ---------------- Signalname
motion.tooloffset.z --------- Ausgang HAL-Pin von LinuxCNC Bewegungsmodul
xyzac-trt-kins.tool-offset -- Eingang HAL-Pin zu xyzac-trt-kins7. Kundenspezifische Kinematik-Komponenten
LinuxCNC implementiert Kinematik mit einer HAL-Komponente, die beim Starten von LinuxCNC geladen wird. Die häufigste Kinematik-Modul, trivkins, implementiert Identität (trivial) Kinematik, wo es eine eins-zu-eins-Korrespondenz zwischen einer Achse Koordinate Buchstaben und einem Motor Gelenk. Zusätzliche Kinematik-Module für komplexere Systeme (einschließlich "xyzac-trt" und "xyzbc-trt" oben beschrieben) sind verfügbar.
Kurze Beschreibungen der verfügbaren Kinematikmodule finden Sie in der kins-Manpage (\$ man kins).
Die Kinematik-Module von LinuxCNC vorgesehen sind in der Regel in der C-Sprache geschrieben. Durch die Verwendung einer Standardstruktur wird die Erstellung eines benutzerdefinierten Kinematik-Moduls erleichter durch das Kopieren einer vorhandenen Quelldatei in eine Benutzerdatei mit einem neuen Namen, ändern Sie den und dann installieren.
Die Installation erfolgt mit halcompile:
sudo halcompile --install kinsname.cwobei "kinsname" der Name ist, den Sie Ihrer Komponente geben. Das sudo-Präfix ist für die Installation erforderlich und Sie werden nach Ihrem root-Passwort gefragt. Weitere Informationen finden Sie in der Manpage von halcompile (\$ man halcompile)
Sobald es kompiliert und installiert ist, können Sie es in der Konfiguration Ihres Rechners referenzieren. Dies geschieht in der INI-Datei Ihres Konfigurationsverzeichnisses. Zum Beispiel die allgemeine INI Spezifikation:
[KINS] KINEMATICS = trivkins
wird ersetzt durch
[KINS] KINEMATICS = kinsname
wobei "kinsname" der Name Ihres kins-Programms ist. Zusätzliche HAL-Pins können vom Modul für variable Konfigurationselemente wie Dx, Dy, Dz, Werkzeug-Offset, die im xyzac-trt-Kinematikmodul verwendet werden, erstellt werden. Diese Pins können mit einem Signal zur dynamischen Steuerung verbunden werden oder einmalig mit HAL-Verbindungen wie:
# Offset-Parameter einstellen net :tool-offset motion.tooloffset.z xyzac-trt-kins.tool-offset setp xyzac-trt-kins.y-versatz 0 setp xyzac-trt-kins.z-versatz 20
8. Abbildungen
9. VERWEISE
-
AXIS MACHINE TOOLS: Kinematik und Vismach-Implementierung in LinuxCNC, RJ du Preez, SA-CNC-CLUB, 7. April 2016.
-
A Postprocessor Based on the Kinematics Model for General Five-Axis machine Tools: C-H She, R-S Lee, J Manufacturing Processes, V2 N2, 2000.
-
NC Post-processor for 5-axis milling of table-rotating/tilting type: YH Jung, DW Lee, JS Kim, HS Mok, J Materials Processing Technology,130-131 (2002) 641-646.
-
3D 6-DOF Serial Arm Robot Kinematics, RJ du Preez, SA-CNC-CLUB, Dec. 5, 2013.
-
Design of a generic five-axis postprocessor based on generalized kinematics model of machine tool: C-H She, C-C Chang, Int. J Machine Tools & Manufacture, 47 (2007) 537-545.