1. Вступ
Координовані багатоосьові верстати з CNC, що керуються за допомогою LinuxCNC, вимагають спеціального кінематичного компонента для кожного типу верстата. У цьому розділі описано деякі з найпопулярніших конфігурацій 5-осьових верстатів, а потім розроблено прямі (від робочих до спільних координат) та обернені (від спільних до робочих) перетворення в загальному математичному процесі для двох типів верстатів.
Наведено кінематичні компоненти, а також моделі вісмаш-симуляції для демонстрації їхньої поведінки на екрані комп’ютера. Також наведено приклади даних HAL-файлу.
Зверніть увагу, що за цієї кінематики осі обертання рухаються у протилежному напрямку відносно прийнятого. Див. розділ ["осі обертання"](https://linuxcnc.org/docs/html/gcode/machining-center.html#_rotational_axes) для деталей.
2. Конфігурації 5-осьових верстатів
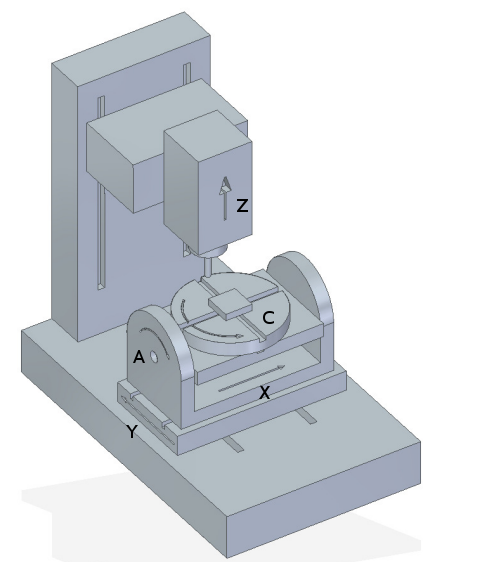
У цьому розділі ми розглянемо типові 5-осьові фрезерні або фрезерні верстати з п’ятьма шарнірами або ступенями вільності, які керуються скоординованими рухами.
3-осьові верстати не можуть змінювати орієнтацію інструменту, тому 5-осьові верстати використовують дві додаткові осі для встановлення ріжучого інструменту у відповідній орієнтації для ефективної обробки поверхонь довільної форми.
Типові конфігурації 5-осьових верстатів показано на рис. 3, 5, 7 та 9-11 [1,2] у розділі Рисунки.
Кінематика 5-осьових верстатів набагато простіша, ніж у 6-осьових серійних роботів з маніпулятором, оскільки 3 осі зазвичай є лінійними осями, а лише дві – осями обертання.
3. Орієнтація та розташування інструменту
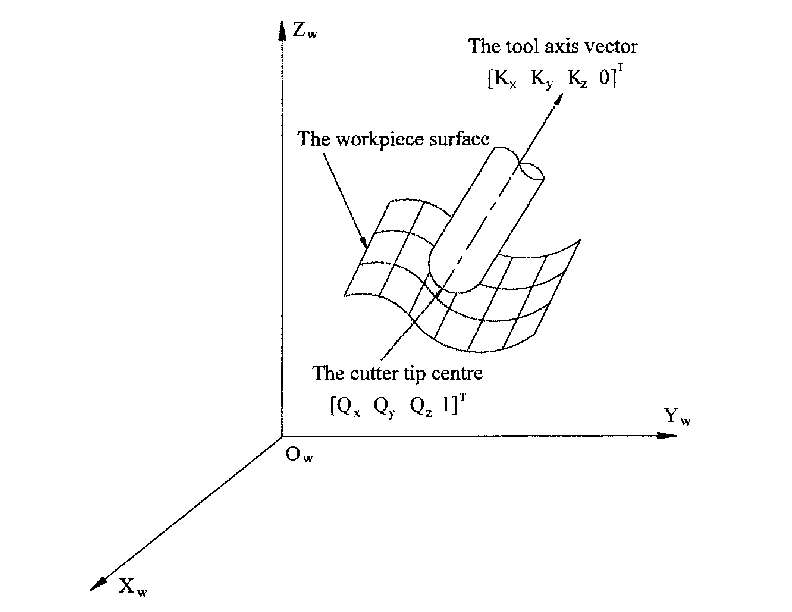
Системи CAD/CAM зазвичай використовуються для створення 3D-моделей заготовки в CAD, а також даних CAM для введення в 5-осьовий верстат з CNC. Дані про розташування інструменту або різака (CL) складаються з положення кінчика різака та орієнтації різака відносно системи координат заготовки. Ця інформація міститься у двох векторах, які генеруються більшістю систем CAM і показані на рис. 1:
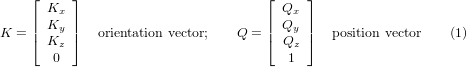
Вектор K еквівалентний 3-му вектору з матриці пози E6, яка використовувалася в 6-осьовій кінематиці робота [3], а вектор Q еквівалентний 4-му вектору E6. Наприклад, у MASTERCAM ця інформація міститься в проміжному вихідному файлі ".nci".
4. Матриці переміщення та обертання
Однорідні перетворення забезпечують простий спосіб опису математики багатоосьової кінематики верстатів. Перетворення простору H є матрицею 4x4 і може представляти перетворення зсуву та обертання. Якщо задано точку x,y,x, описану вектором u = {x,y,z,1}T, то її перетворення v представлено матричним добутком
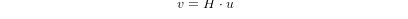
Існує чотири фундаментальні матриці перетворення, на яких може базуватися 5-осьова кінематика:
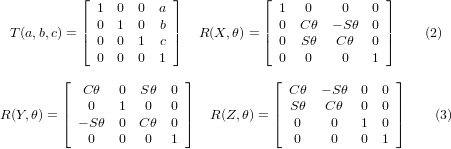
Матриця T(a,b,c) означає зсув у напрямках координат X, Y, Z на величини a, b, c відповідно. Матриці R означають обертання на кут тета навколо осей координат X, Y і Z відповідно. Символи «C» і «S» позначають відповідно косинусну і синусну функції.
5. Поворотні/нахилені 5-осьові конфігурації столу
У цих верстатах дві осі обертання кріпляться на робочому столі верстата. Зазвичай використовуються дві форми:
-
Поворотний стіл, що обертається навколо вертикальної осі Z (поворот C, вторинний), встановлений на нахильному столі, що обертається навколо осі X або Y (поворот A або B, первинний). Заготовка встановлюється на поворотний стіл.
-
Нахильний стіл, що обертається навколо осі X або Y (обертання A або B, вторинне), встановлений на поворотному столі, що обертається навколо осі Z (обертання C, первинне), з заготовкою на нахильному столі.

Багатоосьову машину можна розглядати як сукупність ланок, з’єднаних між собою шарнірами. Вбудувавши систему координат у кожну ланку машини та використовуючи однорідні перетворення, ми можемо описати відносне положення та орієнтацію між цими системами координат
Нам потрібно описати взаємозв’язок між системою координат заготовки та системою координат інструменту. Це можна визначити за допомогою матриці перетворення «wAt», яку можна знайти за допомогою послідовних перетворень між різними структурними елементами або ланками верстата, кожна з яких має свою власну систему координат. Загалом таке перетворення може виглядати наступним чином:

де кожна матриця i-1Aj є матрицею зсуву T або матрицею обертання R виду (2,3).
Множення матриць — це простий процес, при якому елементи кожного рядка лівої матриці A множаться на елементи кожного стовпця правої матриці B і підсумовуються для отримання елемента в матриці результатів C, тобто.
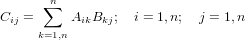
На рис. 2 показано загальну конфігурацію з системами координат [4]. Вона включає осі обертання/нахилу столу, а також осі обертання/нахилу шпинделя. У верстаті фактично використовуються тільки дві осі обертання.
Спочатку ми розробимо перетворення для першого типу конфігурації, згаданого вище, тобто типу нахилу/обертання столу (trt) без зміщення осі обертання. Ми можемо назвати її конфігурацією xyzac-trt.
Ми також розробляємо перетворення для того ж типу (xyzac-trt), але зі зміщеннями осей обертання.
Потім ми розробляємо перетворення для конфігурації xyzbc-trt зі зміщеннями осей обертання.
5.1. Трансформації для верстата xyzac-trt зі зміщеннями робочої точки

Тут ми маємо справу зі спрощеною конфігурацією, в якій вісь нахилу і вісь обертання перетинаються в точці, яка називається точкою обертання, як показано на рис. 4. Тому дві системи координат «Ows» і «Owp» на рис. 2 збігаються.

5.1.1. Пряма трансформація
Перетворення можна визначити послідовним множенням матриць:
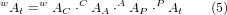
з матрицями, побудованими наступним чином:
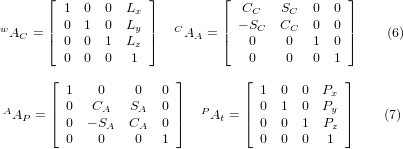
У цих рівняннях Lx, Ly, Lz визначають зміщення точки обертання двох обертових осей A і C відносно початку координат заготовки. Крім того, Px, Py, Pz є відносними відстанями точки обертання до положення кінчика різака, які також можна назвати «координатами з’єднання» точки обертання. Точка обертання знаходиться на перетині двох осей обертання. Знаки членів SA і SC відрізняються від знаків у [2,3], оскільки там обертання столу є від’ємними відносно осей координат заготовки (зауважте, що sin(-theta) = -sin(theta), cos(-theta) = cos(theta)).
При множенні відповідно до (5) отримуємо:
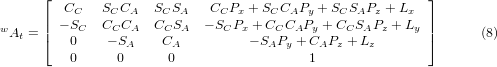
Тепер ми можемо прирівняти третій стовпець цієї матриці до нашого заданого вектора орієнтації інструменту K, тобто:
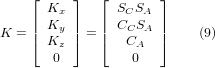
З цих рівнянь ми можемо знайти кути повороту θ⁻⁹A⁻, θ⁻C⁻. З третього рядка знаходимо:
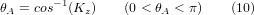
і, поділивши перший рядок на другий рядок, знаходимо:

Ці співвідношення зазвичай використовуються в постпроцесорі CAM для перетворення векторів орієнтації інструменту в кути повороту.
Прирівнюючи останній стовпець (8) до вектора положення інструменту Q, ми можемо записати:
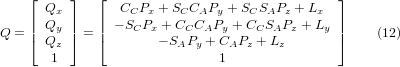
Вектор у правій частині також можна записати як добуток матриці та вектора, що дає:
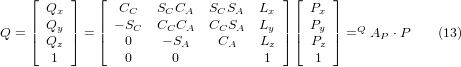
Це можна розширити, щоб надати
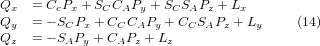
що є «прямим перетворенням» кінематики.
5.1.2. Зворотне перетворення
Ми можемо вирішити P з рівняння (13) як «P = (QAP)-1 * Q». Зазначимо, що квадратна матриця є однорідною матрицею 4x4, що містить матрицю обертання R і вектор перенесення q, для яких обернену матрицю можна записати як:

де R^T — транспонування R (рядки та стовпці поміняні місцями). Таким чином, отримуємо:
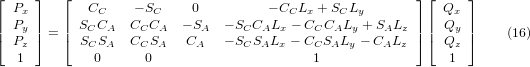
Таким чином, бажані рівняння для «зворотного перетворення» кінематики можна записати так:
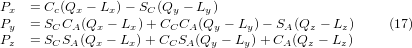
5.2. Перетворення для верстата xyzac-trt зі зміщеннями поворотних осей

Тут ми маємо справу з розширеною конфігурацією, в якій вісь нахилу і вісь обертання не перетинаються в одній точці, а мають зміщення Dy. Крім того, між двома системами координат «Ows» і «Owp» на рис. 2 також існує зміщення по осі z, яке називається Dz. Модель vismach показана на рис. 5, а зміщення показані на рис. 6 (у цьому прикладі зміщення є додатними). Для спрощення конфігурації зміщення Lx, Ly, Lz з попереднього випадку не включені. Вони, ймовірно, не потрібні, якщо використовувати зміщення G54 в LinuxCNC за допомогою функції «touch of».
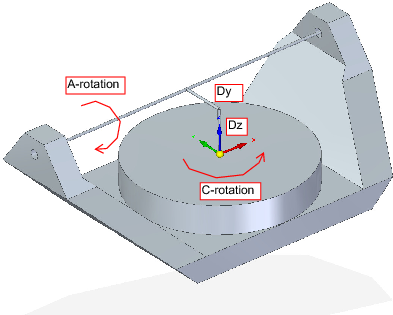
5.2.1. Трансформація вперед
Перетворення можна визначити послідовним множенням матриць:

з матрицями, побудованими наступним чином:
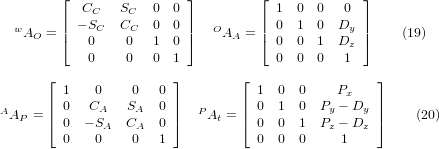
У цих рівняннях Dy, Dz визначають зміщення точки обертання обертових осей A відносно початку координат системи координат заготовки. Крім того, Px, Py, Pz є відносними відстанями точки обертання до положення кінчика різака, які також можна назвати «координатами з’єднання» точки обертання. Точка обертання знаходиться на обертовій осі A.
При множенні відповідно до (18) отримуємо:
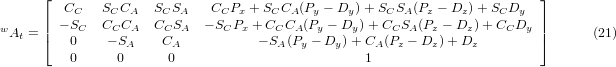
Тепер ми можемо прирівняти третій стовпець цієї матриці до нашого заданого вектора орієнтації інструменту K, тобто:
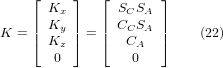
З цих рівнянь ми можемо знайти кути повороту θ⁻⁹A⁻, θ⁻C⁻. З третього рядка знаходимо:
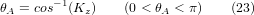
і, поділивши другий рядок на перший рядок, знаходимо:

Ці співвідношення зазвичай використовуються в постпроцесорі CAM для перетворення векторів орієнтації інструменту в кути повороту.
Прирівнюючи останній стовпець (21) до вектора положення інструменту Q, ми можемо записати:
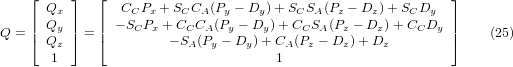
Вектор у правій частині також можна записати як добуток матриці та вектора, що дає:
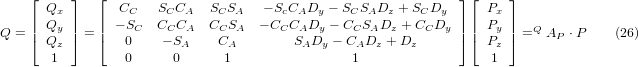
що є «прямим перетворенням» кінематики.
5.2.2. Зворотне перетворення
Ми можемо розв’язати для P рівняння (25) як P = (QAP)-1 * Q, використовуючи (15), як і раніше. Таким чином, ми отримуємо:

Таким чином, бажані рівняння для «зворотного перетворення» кінематики можна записати так:
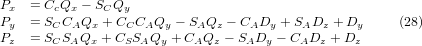
5.3. Перетворення для верстата xyzbc-trt зі зміщеннями поворотних осей

Тут ми знову маємо справу з розширеною конфігурацією, в якій вісь нахилу (навколо осі y) і вісь обертання не перетинаються в одній точці, а мають зміщення Dx. Крім того, між двома системами координат «Ows» і «Owp» на рис. 2 також існує зсув по осі z, який називається Dz. Модель Vismach показана на рис. 7 (у цьому прикладі зсуви від’ємні), а позитивні зсуви показані на рис. 8.
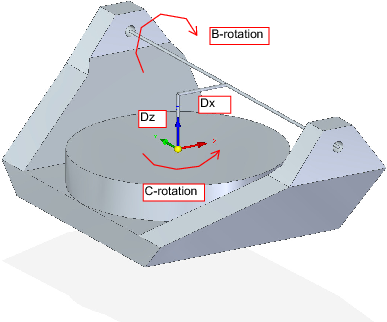
5.3.1. Трансформація вперед
Перетворення можна визначити послідовним множенням матриць:

з матрицями, побудованими наступним чином:
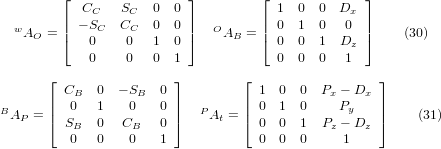
У цих рівняннях Dx, Dz визначають зміщення точки обертання обертових осей B відносно початку координат системи координат заготовки. Крім того, Px, Py, Pz є відносними відстанями точки обертання до положення кінчика різака, які також можна назвати «координатами з’єднання» точки обертання. Точка обертання знаходиться на обертовій осі B.
При множенні відповідно до (29) отримуємо:
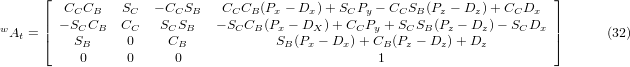
Тепер ми можемо прирівняти третій стовпець цієї матриці до нашого заданого вектора орієнтації інструменту K, тобто:
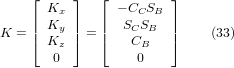
З цих рівнянь ми можемо знайти кути повороту θ⁻⁹B⁻, θ⁻C⁻. З третього рядка знаходимо:

і, поділивши другий рядок на перший рядок, знаходимо:

Ці співвідношення зазвичай використовуються в постпроцесорі CAM для перетворення векторів орієнтації інструменту в кути повороту.
Прирівнюючи останній стовпець (32) до вектора положення інструменту Q, ми можемо записати:

Вектор у правій частині також можна записати як добуток матриці та вектора, що дає:
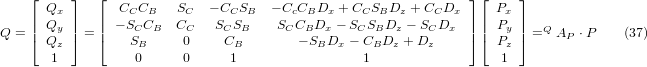
що є «прямим перетворенням» кінематики.
5.3.2. Зворотне перетворення
Ми можемо знайти P з рівняння (37) як P = (QAP)-1 * Q.
Використовуючи той самий підхід, що й раніше, отримуємо:
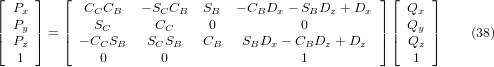
Таким чином, бажані рівняння для «зворотного перетворення» кінематики можна записати так:
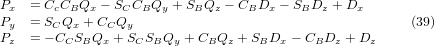
6. Приклади повороту/нахилу столу
LinuxCNC включає кінематичні модулі для топологій «xyzac-trt» та «xyzbc-trt», описаних у математичних розрахунках, наведених вище. Для зацікавлених користувачів вихідний код доступний у дереві git у каталозі «src/emc/kinematics/».
Приклади конфігурацій моделювання xyzac-trt та xyzbc-trt знаходяться в каталозі Зразки конфігурацій (configs/sim/axis/vismach/5axis/table-rotary-tilting/).
Приклади конфігурацій містять необхідні INI-файли та підкаталог з прикладами файлів G-коду (NGC). Ці конфігурації симулятора викликають реалістичну тривимірну модель за допомогою засобу LinuxCNC vismach.
6.1. Моделі моделювання Vismach
Vismach — це бібліотека процедур Python для відображення динамічної симуляції верстата з ЧПК на екрані ПК. Скрипт Python для конкретного верстата завантажується в HAL, а дані передаються через з’єднання контактів HAL. Модель Vismach, що не працює в режимі реального часу, завантажується за допомогою команди HAL, наприклад:
loadusr -W xyzac-trt-gui
а з’єднання встановлюються за допомогою команд HAL, таких як:
net :table-x joint.0.pos-fb xyzac-trt-gui.table-x
net :saddle-y joint.1.pos-fb xyzac-trt-gui.saddle-y
...Дивіться INI-файли симуляції для отримання детальної інформації про HAL-з’єднання, що використовуються для моделі vismach.
6.2. Компенсація довжини інструменту
Для послідовного використання інструментів з таблиці інструментів з автоматичною компенсацією довжини інструменту необхідне додаткове зміщення по осі Z. Для інструменту, який довше за «основний» інструмент, який зазвичай має довжину інструменту нуль, LinuxCNC має змінну під назвою «motion.tooloffset.z». Якщо ця змінна передається до кінематичного компонента (і скрипту vismach python), то необхідне додаткове зміщення по осі Z для нового інструменту можна врахувати, додавши оператор компонента, наприклад:
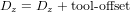
Необхідне HAL-з’єднання (для xyzac-trt):
net :tool-offset motion.tooloffset.z xyzac-trt-kins.tool-offset
де:
:tool-offset ---------------- назва сигналу
motion.tooloffset.z --------- вивід HAL-виводу з модуля руху LinuxCNC
xyzac-trt-kins.tool-offset -- введення HAL-виводу до xyzac-trt-kins7. Компоненти кінематики на замовлення
LinuxCNC реалізує кінематику за допомогою компонента HAL, який завантажується під час запуску LinuxCNC. Найпоширеніший кінематичний модуль, «trivkins», реалізує ідентичну (тривіальну) кінематику, де існує однозначна відповідність між літерою координати осі та з’єднанням двигуна. Доступні додаткові модулі кінематики для більш складних систем (включаючи «xyzac-trt» і «xyzbc-trt», описані вище).
Дивіться сторінку довідки kins (\$ man kins) для отримання коротких описів доступних модулів кінематики.
Модулі кінематики, що надаються LinuxCNC, зазвичай написані мовою C. Оскільки використовується стандартна структура, створення власного модуля кінематики спрощується шляхом копіювання існуючого вихідного файлу в файл користувача з новою назвою, його модифікації та подальшої інсталяції.
Встановлення виконується за допомогою halcompile:
sudo halcompile --install kinsname.cде «kinsname» — це ім’я, яке ви надаєте своєму компоненту. Для його встановлення необхідний префікс sudo, і вам буде запропоновано ввести пароль адміністратора. Докладнішу інформацію див. на сторінці довідки halcompile (\$ man halcompile)
Після компіляції та встановлення ви можете звернутися до нього в конфігурації вашої машини. Це робиться у файлі INI вашого каталогу конфігурації. Наприклад, загальна специфікація INI:
[KINS] KINEMATICS = trivkins
замінюється на
[KINS] KINEMATICS = kinsname
де «kinsname» — це назва вашої програми kins. Модуль може створити додаткові контакти HAL для змінних елементів конфігурації, таких як Dx, Dy, Dz, tool-offset, що використовуються в модулі кінематики xyzac-trt. Ці контакти можна підключити до сигналу для динамічного керування або встановити один раз за допомогою підключень HAL, наприклад:
# встановити параметри зміщення net :tool-offset motion.tooloffset.z xyzac-trt-kins.tool-offset setp xyzac-trt-kins.y-offset 0 setp xyzac-trt-kins.z-offset 20
8. Цифри


9. ПОСИЛАННЯ
-
ОСЕВІ ВЕРСТАТИ: Кінематика та реалізація Vismach у LinuxCNC, Р. Дж. дю Пріз, SA-CNC-CLUB, 7 квітня 2016 р.
-
Постпроцесор на основі кінематичної моделі для загальних п’ятиосьових верстатів: C-H She, R-S Lee, J Manufacturing Processes, V2 N2, 2000.
-
Постпроцесор з NC для 5-осьового фрезерування з поворотним/нахиленим столом: YH Jung, DW Lee, JS Kim, HS Mok, J Materials Processing Technology, 130-131 (2002) 641-646.
-
Кінематика 3D-робота з 6 ступенями свободи на серійній основі, RJ du Preez, SA-CNC-CLUB, 5 грудня 2013 р.
-
Проектування типового п’ятиосьового постпроцесора на основі узагальненої кінематичної моделі верстата: C-H She, C-C Chang, Int. J Machine Tools & Manufacture, 47 (2007) 537-545.